[한글커널] PORTO SEGURO: 운전자 보험 청구 예측 EDA for Korean Part. 3

본 커널은 Porto Seguro의 금메달 EDA 커널을 쉽게 이해하도록 작성한 Korean Starter들을 위한 커널입니다.

 

대부분의 내용은 이미 공개되어 있는 커널이며 이해하기 쉽게 한글로 번역, 설명을 추가한 커널입니다 참고 부탁드립니다.

 

본 커널은 비식별 Feature를 사용하는 대회의 EDA를 위한 커널로, 모델링 및 submission은 진행하지 않습니다.

초보자의 입장에서 초보자분들을 위해 커널을 작성하는 만큼, 쉽게 설명하고자 하였습니다.

 

데이터를 이해함에 있어서 큰 도움을 주신 참고 코드 작성자 분께 감사합니다 :)

 

금메달 커널 원본: https://www.kaggle.com/bertcarremans/data-preparation-exploration

Data Preparation & Exploration

작성자 커널 원본: https://www.kaggle.com/kongnyooong/porto-eda

PORTO SEGURO: EDA for Korean (한글커널)

< 캐글 커널 원본입니다! 하나의 Upvote가 더 좋은 커널을 만드는 원동력이 됩니다 :) >

Part3는 Part2에 이은 EDA에 대해 다뤄볼 예정입니다.

 

Part2을 아직 안보고 오신 분들께서는 여기를 먼저 보고 와주시는게 좋을 것 같습니다! 

 

범주형 변수의 유니크값 확인

• 이 대회는 범주형 변수가 전부 숫자로 매핑되어있습니다.
• 범주형 변수의 유니크 값과 몇개의 유니크 값이 있는지 확인해보겠습니다.

# 이 커널에서는 이런식으로 유니크값이 몇개있는지 확인했다.

Nominal = meta[(meta["level"] == 'nominal') & (meta["keep"])].index

for f in Nominal:
    dist_values = df_train[f].value_counts().shape[0]
    print('Variable {} has {} distinct values'.format(f, dist_values))

 

커널 원본과 다르게 nunique를 사용하면 훨씬 더 편리하게 확인할 수 있을것이라고 생각하여 코드를 한줄 줄여보았습니다.

출력결과는 동일하지만 코드가 단순화되어 더욱 간편합니다.

Nominal = meta[(meta["level"] == 'nominal') & (meta["keep"])].index

for f in Nominal:
    print('Variable {} has {} distinct values'.format(f, df_train[f].nunique()))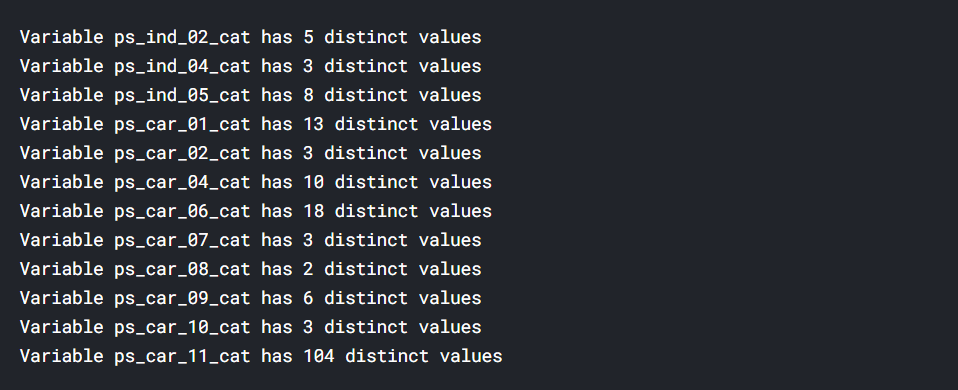

범주형 변수 인코딩

• 범주형 변수를 인코딩하는 방법에서 일반적으로 one-hot-encoding, Label-encoding 방법을 사용합니다.
• 두 가지 방법이 어떻게 이루어지는지는 생략하고 진행하겠습니다.
• one-hot-encoding은 변수에 순서(높고 낮음)이 부여되지 않기 때문에 target을 예측하는데 영향을 주진 않지만 unique값이 많을 경우 굉장히 sparse한 벡터가 생성되고, 또한 faeture도 기하급수적으로 늘어나기 때문에 cost가 늘어나고 차원의 저주에 빠질 확률이 높아지게 됩니다.
• Label-encoding의 경우 feature가 유지되기 때문에 cost가 적고 차원을 신경쓸 필요가 없지만 각각 unique 값에 매핑되는 숫자에 순서가 생겨버리기 때문에 target 예측에 영향을 줄 수 있습니다.
• 이 커널에서는 mean-encoding이라는 방법을 사용했습니다.

mean-encoding

• 어떻게 이루어지는에 대한 설명은 아래 예시와 같습니다.
• 캐글에서는 mean encoding, frequency encoding 등 방법들을 많이 사용한다고 합니다.
• 차원의 저주에 빠질 확률이 없고 빠르다는 장점이 있습니다.
• 가장 큰 장점으로는 target과의 mean을 취해주었기 때문에 일종의 상관관계를 가지게 됩니다.
• 하지만 치명적인 단점이 있습니다.
• 바로 Data Leakage 문제와 오버피팅 문제입니다.
• test 및 추후 수집될 데이터 셋에 대한 target 값을 알지 못하기 때문에 target에 대한 평균을 train 데이터 셋으로만 적용시켜야 합니다.
• 그렇기 때문에 test 셋의 target 값을 사용하게 되면 data leakage 문제에 빠지게되고, train 셋의 target 값만 사용하게 되면 오버피팅되는 딜레마가 있습니다.
• 특히 train, test 셋의 unique값 분포가 크게 다를 때 오버피팅 문제는 커지게 됩니다.
• ex. train 셋의 남자 95명 여자5명, test 셋의 남자 50명, 여자 50명

단점을 어떻게 극복하는가?

• 이러한 단점들을 완화시키기 위한 방법들이 여러가지 있습니다.
  1) smoothing
  2) CV
  3) Expanding mean
  출처: https://dailyheumsi.tistory.com/120   

mean-encoding 예시

# 아래와 같은 데이터가 있다고 가정해보자

ex_list = [("남자", 1), ("여자", 1), ("여자", 1), ("여자", 0), ("남자", 0)]

ex = pd.DataFrame(data = ex_list, columns = ["성별", "target"])

# 이런 방법으로 인코딩을 수행한다.
# 인코딩할 범주형 변수와 target을 groupby해준 후 평균값을 취해준다.

성별_mean = ex.groupby("성별")["target"].mean()

# 그렇게 되면 아래와 같은 값을 얻을 수 있다.
# 남자의 경우 2개의 데이터에서 target값이 1과0 이므로 0.5가 나오고,
# 여자의 경우 3개의 데이터에서 target값이 1이 2개 0이 1개이므로 0.6667이 나온다.
# 이 값으로 해당 unique값을 인코딩 해준다.

성별_mean

아래는 커널에서 구현한 mean-encoding 코드입니다.

코드가 매우 복잡해보이지만 결국 위에서 보았던 예제 방식을 구현한 것입니다.

커널에서는 오버피팅 방지를 위해 noise를 추가하고, smoothing을 적용하기 때문에 코드가 복잡해보입니다

smoothing을 통해 평균값이 치우친 상황을 조금이나마 보완해줄 수 있습니다. (전체 평균값으로 가깝게)

smoothing에 대한 자세한 이론은 위의 설명에 있는 출처 링크에서 참고하시면 됩니다!

def add_noise(series, noise_level):
    return series * (1 + noise_level * np.random.randn(len(series)))

def target_encode(trn_series=None, 
                  tst_series=None, 
                  target=None, 
                  min_samples_leaf=1, 
                  smoothing=1,
                  noise_level=0):
    assert len(trn_series) == len(target)
    assert trn_series.name == tst_series.name
    temp = pd.concat([trn_series, target], axis=1)
    # agg를 사용해서 평균값을 구해줌
    averages = temp.groupby(by=trn_series.name)[target.name].agg(["mean", "count"])
    # 오버피팅 방지를 위한 smoothing
    smoothing = 1 / (1 + np.exp(-(averages["count"] - min_samples_leaf) / smoothing))
    prior = target.mean()
    averages[target.name] = prior * (1 - smoothing) + averages["mean"] * smoothing
    averages.drop(["mean", "count"], axis=1, inplace=True)
    # train, test에 적용시켜준다.
    ft_trn_series = pd.merge(
        trn_series.to_frame(trn_series.name),
        averages.reset_index().rename(columns={'index': target.name, target.name: 'average'}),
        on=trn_series.name,
        how='left')['average'].rename(trn_series.name + '_mean').fillna(prior)
    ft_trn_series.index = trn_series.index 
    ft_tst_series = pd.merge(
        tst_series.to_frame(tst_series.name),
        averages.reset_index().rename(columns={'index': target.name, target.name: 'average'}),
        on=tst_series.name,
        how='left')['average'].rename(trn_series.name + '_mean').fillna(prior)
  
    ft_tst_series.index = tst_series.index
    return add_noise(ft_trn_series, noise_level), add_noise(ft_tst_series, noise_level)

# 위에서 구현한 함수를 ps_car_11_cat(104개의 유니크 값)에 적용시켜준다.
# feature가 바뀌었으므로 메타데이터를 업데이트 해준다.

train_encoded, test_encoded = target_encode(df_train["ps_car_11_cat"], 
                             df_test["ps_car_11_cat"], 
                             target=df_train.target, 
                             min_samples_leaf=100,
                             smoothing=10,
                             noise_level=0.01)
    
df_train['ps_car_11_cat_te'] = train_encoded
df_train.drop('ps_car_11_cat', axis=1, inplace=True)
meta.loc['ps_car_11_cat','keep'] = False  
df_test['ps_car_11_cat_te'] = test_encoded
df_test.drop('ps_car_11_cat', axis=1, inplace=True)

시각화를 통한 데이터 탐색

범주형 변수 시각화

target이 1인 범주형 변수들의 특성을 시각화를 통해 파악해보겠습니다.

Nominal = meta[(meta["level"] == 'nominal') & (meta["keep"])].index


# 변수별로 반복문을 돌려서 barplot을 그린다.
for f in Nominal:
    plt.figure()
    fig, ax = plt.subplots(figsize=(20,10))
    ax.grid(axis = "y", linestyle='--')
    # 변수 별 target=1의 비율 계산
    cat_perc = df_train[[f, 'target']].groupby([f],as_index=False).mean()
    cat_perc.sort_values(by='target', ascending=False, inplace=True)
    
    # 위에서 계산해준 비율을 통해 target = 1의 데이터 중 어떤 유니크값의 비율이 높은지 확인할 수 있다.
    sns.barplot(ax=ax, x=f, y='target',palette = "Pastel1", edgecolor='black', linewidth=0.8, data=cat_perc, order=cat_perc[f], )
    plt.ylabel('% target', fontsize=18)
    plt.xlabel(f, fontsize=18)
    plt.tick_params(axis='both', which='major', labelsize=18)
    plt.show();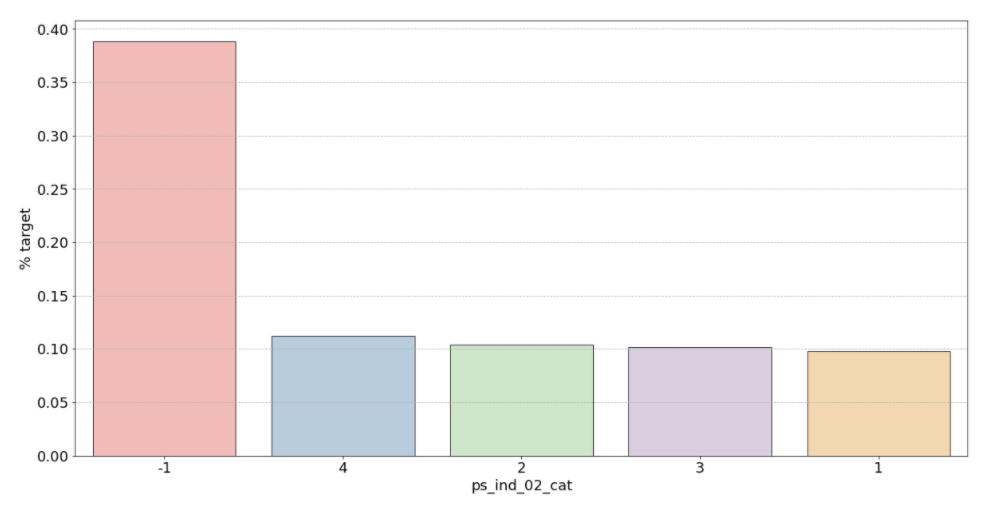

범주형 변수 시각화 결과 확인

• 주의해야할 점: 이 커널에서 시각화한 barplot만 놓고 보면 잘못된 인사이트를 얻을 수 있습니다. (단순 비율로만 계산하고 count 값은 고려하지 못하므로, 특히 위에서 확인했듯이 결측치가 많은 것은 대체해줬으므로 -1 값의 count는 작은것 밖에 남지 않았음)
• 추가로 생각해보면 좋을 점: 보통 범주형변수의 countplot이나 barplot을 그릴때 groupby(hue를 지정)하여 살펴보면 어떤 Feature를 만들 수 있을지 생각해볼 수 있고, 더 다양한 인사이트를 얻을 수 있습니다.

1) ps_ind_02_cat: -1(결측치)의 경우 target = 1의 데이터가 40%를 차지합니다. 나머지는 10% 정도로 보입니다.
여기서 주의해야할 점은 높다고 좋은게 아니라는 것입니다 (target에 대한 비율이기 때문에 50%에 가까울수록 애매한 unique 값이라는 뜻)
차라리 10%를 보이는 나머지 unique 값들이 보험 청구를 안할 확률이 높다는 뜻이므로 오히려 확실한 정보라고 할 수 있습니다.

2) ps_ind_04_cat: -1(결측치)가 65% 정도로 target = 1의 값을 가집니다. 보험을 청구할 확률이 높아보입니다.

3) ps_ind_05_cat: unique 값 마다 차이가 있지만 눈에 띄는 unique 값은 없습니다.

4) ps_car_01_cat: -1(결측치)가 거의 50%에 가까우므로 애매하다고 할 수 있습니다. 나머지 값은 다 보험을 청구하지 않을 확률이 높아보입니다.

5) ps_car_02_cat: -1(결측치)가 0%입니다. 보험을 절대 청구하지 않을 것으로 보입니다.

6) 그 외: unique 값 마다 어느정도 차이들을 보입니다.

일단 커널을 따라가도록 하겠습니다.
커널에 따르면 결측값이 특이한 경우가 많으므로 대체하기 보다 그냥 두는게 나을것 같다고 판단하였습니다.

Interval 변수 시각화 (연속형)

• heatmap으로 상관관계 파악

def corr_heatmap(Interval):
    correlations = df_train[Interval].corr()

    # Create color map ranging between two colors
    cmap = sns.diverging_palette(220, 10, as_cmap=True)

    fig, ax = plt.subplots(figsize=(10,10))
    sns.heatmap(correlations, cmap=cmap, vmax=1.0, center=0, fmt='.2f',
                square=True, linewidths=.5, annot=True, cbar_kws={"shrink": .75})
    plt.show();
    
Interval = meta[(meta["role"] == "target") | (meta["level"] == 'interval') & (meta["keep"])].index
corr_heatmap(Interval)

몇개의 변수들은 강한 상관관계를 보입니다.

• ps_reg_02 & ps_reg_03 (0.7)
• ps_car_12 & ps_car13 (0.67)
• ps_car_12 & ps_car14 (0.58)
• ps_car_13 & ps_car15 (0.67)

살펴본 강한 상관관계를 가지는 변수들에 대해 추가로 시각화를 진행하도록 하겠습니다.

1) ps_reg_02 & ps_reg_03

• plot을 보면 두 개의 변수가 선형관계를 이루는 것을 확인할 수 있습니다.
• 회귀선이 겹치거나 비슷한 모습입니다.

sns.lmplot(x='ps_reg_02', y='ps_reg_03', data=df_train, hue='target', palette='Set1', scatter_kws={'alpha':0.3})
plt.show()

ps_car_12 & ps_car_13

sns.lmplot(x='ps_car_12', y='ps_car_13', data=df_train, hue='target', palette='Set1', scatter_kws={'alpha':0.3})
plt.show()

ps_car_12 and ps_car_14

sns.lmplot(x='ps_car_12', y='ps_car_14', data=df_train, hue='target', palette='Set1', scatter_kws={'alpha':0.3})
plt.show()

ps_car_13 & ps_car_15

sns.lmplot(x='ps_car_15', y='ps_car_13', data=df_train, hue='target', palette='Set1', scatter_kws={'alpha':0.3})
plt.show()

Ordinal 변수 시각화

• heatmap으로 상관관계 파악해봅니다.
• 순서형 변수의 경우 변수간에 큰 상관관계를 보이지 않는 것으로 확인됩니다.

Ordinal = meta[(meta["role"] == "target") | (meta["level"] == 'ordinal') & (meta["keep"])].index
corr_heatmap(Ordinal)

Feature Engineering

• 위에서 가장 많은 unique 값을 갖는 범주형 변수에 대해서 mean-encoding을 해주었습니다.
• 나머지 변수들은 one-hot encoding 해주어 더미화 시켜줍니다
• 범주형 변수에 순서도 부여하지 않고, unique 값도 많지 않아 차원이 많이 늘어나지도 않습니다.

Nominal = meta[(meta["level"] == 'nominal') & (meta["keep"])].index
print('One-Hot Encoding 전 train 데이터 셋 변수 개수: {}'.format(df_train.shape[1]))
df_train = pd.get_dummies(df_train, columns=Nominal, drop_first=True)
df_test = pd.get_dummies(df_test, columns=Nominal, drop_first=True)
print('One-Hot Encoding 후 train 데이터 셋 변수 개수: {}'.format(df_train.shape[1]))

# 52개의 변수가 늘어났다.

교호작용 변수 생성 (중요 변수끼리의 곱)

• PolynomialFeatures를 사용하여 교호작용 변수를 생성합니다.
• 입력값 x를 다항식으로 변환 (x >> [1, x, x^2, x^3...])
• 열의 개수가 2개라면 (x1, x2 >> [1, x1, x2, x1^2, x2^2, x1x2])
• poly.get_feature_names를 통해 편하게 feature의 이름을 지정해줄 수 있습니다.

Parameter

1. degree: 차수
2. interaction_only: 상호작용 항만 출력 (x1, x2일 때 자신의 제곱항은 무시하고 x1x2 만 출력)
3. include_bias: 상수항 생성 여부

Interval = meta[(meta["level"] == 'interval') & (meta["keep"])].index

poly = PolynomialFeatures(degree=2, interaction_only=False, include_bias=False)
interactions = pd.DataFrame(data=poly.fit_transform(df_train[Interval]), columns=poly.get_feature_names(Interval))
interactions.drop(Interval, axis=1, inplace=True)  # interactions 데이터프레임에서 기존 변수 삭제

# 새로 만든 변수들을 기존 데이터에 concat 시켜줌
print('교호작용 변수 생성 전 train 데이터 셋 변수 개수: {}'.format(df_train.shape[1]))
df_train = pd.concat([df_train, interactions], axis=1)
df_test = pd.concat([df_test, interactions], axis=1)
print('교호작용 변수 생성 후 train 데이터 셋 변수 개수: {}'.format(df_train.shape[1]))

여기까지 본 커널의 코드는 끝이납니다! 

 

해당 대회의 주요한 Feature Engineering과 Modeling은 다루지 않았지만, 마스킹된 변수들을 하나하나 살펴보면서 EDA를 진행하는 과정을 거쳤습니다.

 

마무리로 상위 커널의 Discussion를 살펴보며 포스팅을 마치겠습니다.

 

상위커널 Discussion

• 캐글의 경우 금메달 커널은 리뷰하는 것도 굉장히 도움이 많이 되지만, 정말 알짜 정보들은 Discussion에 많이 몰려있습니다.
• 당연히 대회가 끝나기 전에는 Solution이 올라오지는 않지만, Discussion에서 확인할 수 있는 작은 인사이트들이 큰 도움이 되는 경우가 많습니다.

1등 Discussion 정리

1) 모델: LightGBM, NeuralNet 사용 (오토인코더: 비지도 학습 기반 뉴럴 넷, 이미지 복원등에 주로 사용, 노이즈 제거에 특화되어 있음)

• Discussion과 상위 커널 몇개를 살펴본 결과 노이즈를 처리하는 것이 대회의 핵심이었던것 같습니다.
• 그래서 대회 우승자들은 일반적인 머신러닝 모델 + 딥러닝 모델을 사용한것으로 보입니다.
• 오토인코더 참고: https://sunghan-kim.github.io/ml/3min-dl-ch08/#

2) FE: cals 변수 제거, cat 변수 one-hot encoding

• 딱히 많은 파생변수를 만들어내지 않았음에도 1등을 차지했습니다. (데이터의 특성에 맞는 모델을 사용한 결과)

3) Scaling: 일반 트리모델이 아닌 딥러닝 모델을 사용하였기 때문에 필수적으로 사용 (RankGauss라는 기법을 사용했다고 합니다.)

• RankGauss라는 기법은 본 커널을 통해 처음 알게된 방법입니다. 
• 이런 새로운 기법을 알아가고 공부할 수 있는 것이 캐글을 하는 이유가 아닐까 싶습니다 :)
• RankGauss 참고: https://github.com/aldente0630/gauss_rank_scaler

3등 Discussion 정리

1) 모델: LightGBM, NeuralNet 사용 (역시 오토인코더 사용)

2) FE: 머신러닝 모델에서
['ps_ind_14', 'ps_car_10_cat', 'ps_car_14', 'ps_ind_10_bin', 'ps_ind_11_bin','ps_ind_12_bin', 'ps_ind_13_bin', 'ps_car_11', 'ps_car_12']
이 변수들을 삭제했다고합니다. (교차검증 점수 확인하며 삭제)

• one-hot encoding이 노이즈를 줄이는데 도움이 되었다고 합니다.

3) 아쉬웠던 점은, 이상치를 제대로 파악하지 못했다고 합니다.

• 위의 EDA에서 살펴보았던 count는 적지만 1으로 분류될 확률이 엄청 높았던 -1(결측치)라든지 그런 부분을 이야기하는 것 같습니다.

이상으로 PORTO SEGURO 한글커널 포스팅을 마치도록 하겠습니다 감사합니다!